Particle Swarm Optimization

Particle Swarm Optimization (PSO) is a type of algorithm that is used to find the best solution to a problem. The algorithm works by simulating the behavior of a group of particles, such as birds or fish, that move through a space and interact with each other to find the best solution.

Each particle represents a potential solution to the problem and has a position and a velocity. The algorithm starts with a group of randomly positioned particles. Each particle then moves through the space, updating its position based on its current velocity and the positions of the other particles. The goal is for the particles to converge on the best solution, which is the global optimum of the function being optimized.

The algorithm uses two main parameters: the cognitive component, which is based on the particle's own best position, and the social component, which is based on the best position of the other particles. These two components are used to update the particle's velocity and position, and the algorithm continues to iterate until the particles converge on the best solution.

In summary, PSO is a computational method that simulates the behavior of a group of particles, each representing a potential solution, that move through a space and interact with each other to find the global optimum of a function in a multi-dimensional space

Introduction

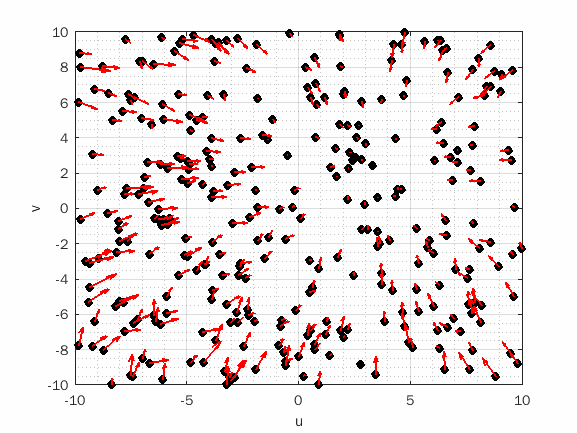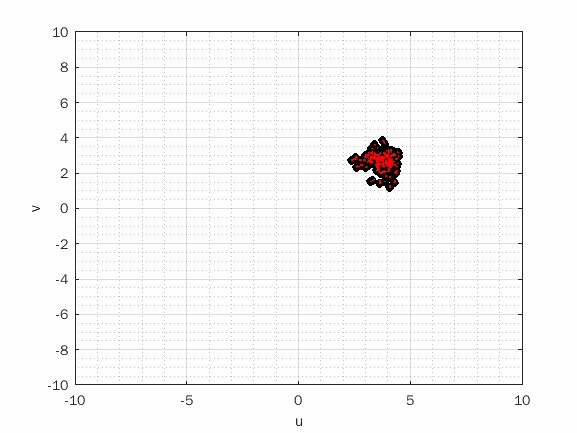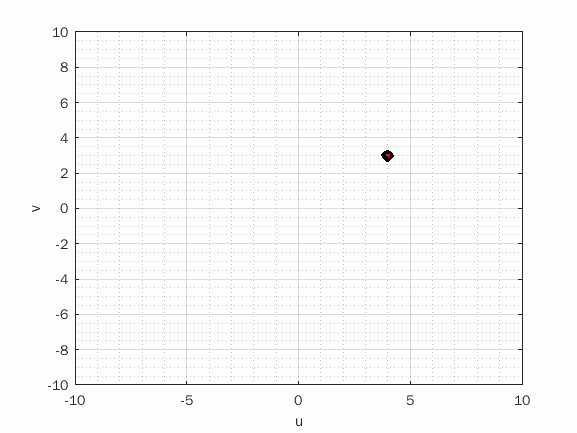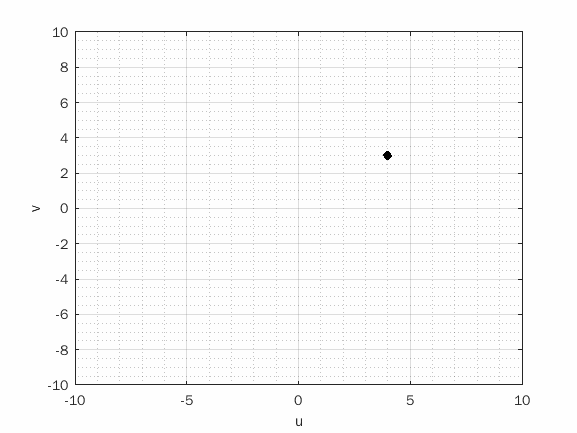There are several ways to maximize or minimize a function to find the optimum. To establish whether an optimization method is suitable for a problem, different aspects influence, such as concavity and differentiability of the function. The particle swarm optimization algorithm (PSO) proposed by Kennedy and Eberhart in 1995^[1] is an algorithm based on the concept of swarm intelligence, generally observed in groups of animals such as fish shoals and herds.

Kennedy and Eberhart, inspired by the social behavior of birds, which grants them a great survival advantage when solving the problem of finding a safe place to land, proposed an algorithm that mimics this behavior. Compared to other optimization algorithms, PSO has some advantages because it has few tuning parameters and they are widely discussed in the literature. From the initial version of the algorithm, new formulations were developed. This note covers the classic version of PSO, also known as the inertial version.

Working Principles

The objective of an optimization problem is to determine the variable represented by a vector X = [x₁, x₂, x₃, ... ,x_n] where n is the number of variables to the determined in the problem, that minimizes or maximizes the objective function f(X). For the PSO algorithm, considering a swarm of P particles, there is a position vector X_i^t=(x_i1 x_i2 ... x_in) and a velocity vector V_i^t=(v_i1 v_i2 ... v_in)in the t^th iteration for each i^th particle that composes them. These vectors are updated for j dimensions according to the equations:

V_ij^t+1 = wV^t_ij + c₁r₁^t(pbest_ij - X_ij^t)+c₂r₂^t(gbest_j - X^t_ij),

X_ij^t+1 = X_ij^t + V_ij^t,

where i = 1, 2, ..., P and j = 1, 2, ..., n. Thus, there are three different factors that contribute to the velocity and, consequently, the movement of a particle in each iteration.

In the first term, the parameter w is the inertial weight, which for the classical algorithm is a positive constant value. This parameter propagates the previous motion to the current instant by multiplying the previous velocity of the particle in the velocity update equation. This means that when w=1 the particle is totally influenced by the previous velocity, keeping the particle in the same direction. Whereas, if w ≤ 0 < 1, this influence is reduced, so the particle can move in more directions. Then, as the inertial weight parameter is reduced, the swarm can explore more areas in the search domain, not depending so much on the previous velocity, increasing the chances of finding a global optimum. On the other hand, the algorithm takes longer to run. The reduction of the value of the inertial parameter w over time was an interesting way found for the particles to start their movement by exploring different areas in the search domain, progressively converging to the global minimum (or maximum) point.

The second term, called individual cognition, is formed by the difference between the best position that the particle has ever occupied and the current position, serving to attract the particle to its best position. The parameter c₁ is a positive constant and weighs the importance of the particle's previous experiences. The r₁ parameter is a uniform random value in the [0,1] interval and serves to avoid premature convergences, increasing the chances of finding a global optimum.

The last term represents social learning. It is a way for particles to share information about the best point reached by any of them. The constant c₂ is the social learning parameter that weighs the importance of the swarm's global learning. Parameter r₂ has the same role as r₁ and also has uniform distribution over the interval [0,1].

Figure 1 shows a particle at position X_ij^t and velocity V_ij^t and Figure 2 illustrates how the particle's position and velocity update process takes place.

Figure 1 - Particle

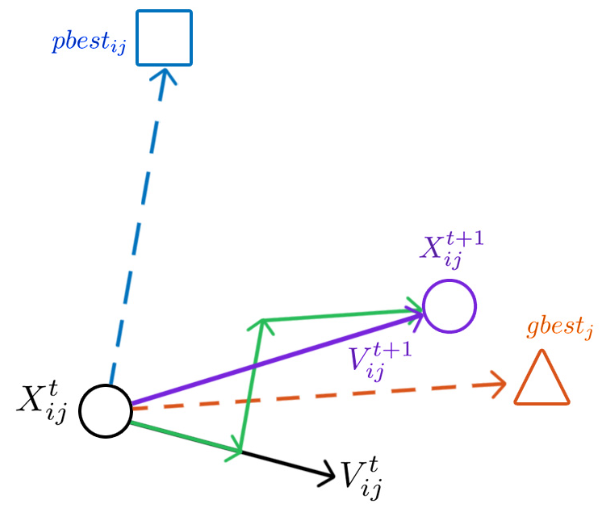
Figure 2 - Position and velocity update process

References

[1] James Kennedy and Russell Eberhart. Particle swarm optimization. In Proceedings of ICNN'95 International Conference on Neural Networks. Vol. 4. IEEE. 1995, pp. 1942-1948.